What is Finite Automata?|| DFA , NFA ||
Basic Concept:
The finite state system represents a mathematical model of a system with certain input. The model finally gives certain output. The input when is given to the machine it is processed by various states, these state are called as intermediate states.
The very good example of finite state system is a control mechanism of elevator. This mechanism only remembers the current floor number pressed, it does not remember all the previously pressed numbers.
The finite state system is a very good design tool for the programs such as text editors and lexical analyzers (which is used in compilers). The lexical analyzers is a program which cans your program character by character and recognizes those words as tokens.
Definition of Finite Automata(FA):
A finite automata is a collections of 5-tuple ( Q , Σ , δ , q0 , F )
where,
Q is a finite set of state, which is non empty.
Σ is input alphabet, indicates input set.
q0 is an initial state and q0 is in Q i.e. Є Q.
F is a set of final states.
δ is a transition function or a mapping function. Using this function the next state can be determined.
Finite Automata Model:
The finite automata cab be represented as :
 |
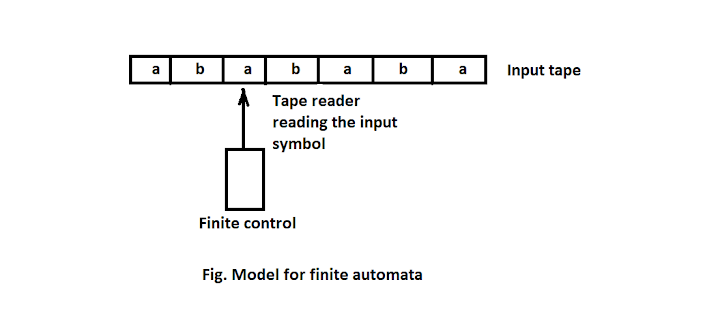| Model for finite automata |
The finite automata can be represented using
i). Input tape :- It is linear tape having some number of cells. Each input symbol is placed in each cell.
ii). Finite control :- The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right and at a time only one input symbol is read.
For example, suppose current state is q, and suppose reader is reading the symbol 'a' then it is finite control which decides what will be the next state at input 'a' The transition from current state q with input w to next state q' producing w' will be represented as,
(q, w) |- (q', w')
If w is a string and M is a automata, than w is accepted by the FA.
iff (w, s) |-* (q , ε )
with q as final state.
The set of string accepted by FA given by M is accepted by language L. The acceptance of M by some language L is denoted by L(M).
A machine M by accepts a language L iff,
L = L(M).
Types of Automata:
There are two types of finite automata
- Deterministic Finite Automata.
- Non deterministic Finite Automata/
1. Deterministic Finite Automata (DFA):
The finite automata is called Deterministic Finite Automata if there in only one path for a specific input from current state to next state. For example, the DFA can be shown as below.
 |
| Deterministic Finite Automata |
From state S0 for input 'a' there is only one path, going to S2. Similar from S0 there is only one path for input b going to S1.
The DFA can be represented by the same 5-tuples described in the definition of FSM. All the above example are actually the DFAs.
Definition of DFA:
A deterministic finite automata is a collection of following things -
- The finite set of state which can be denoted by Q.
- The finite set of input symbols Σ.
- The start state q0 such that q0 Є Q.
- A set of final state F such that F Є Q.
- The mapping function or transition function denoted by δ. Two parameters are passed to this transition function : One is current state and other is input symbol. The transition function returns a state which can be called as next state.
In short , the DFA is a five tuple notation denoted as :
A = (Q , Σ , δ , q0 , F )
The name of DFA is A which is a collection of above describe five elements.
➡ Example : Design a FA which accepts the only input 101 over the input set Z = { 0 ,1 }
Solution: 
Note that in the problem statement it is mentioned as only input 101 will be accepted. Hence in the solution we have simply shown the transitions, for input 101. There is no other path shown for other input.
Non deterministic Finite Automata (NFA):
The concept of Non deterministic finite automata is exactly reverse of Deterministic finite automata. The Finite Automata is called NFA When there exists many paths for a specific input from current state to next state. The NFA can be shown as
Note that the NFA shows from q0 for input a there are two next state q1 and q2 similarly, from q0 for input b the next state are q0 and q1.
Thus it is not fixed or that with a particular input where to go next. Hence this FA is called non deterministic finite automata.
Consider the input string bba. This string can be derived as
Input b b a
path q0 q0 q1
or input b b a
path q0 q0 q2
or Input b b a
path q0 q1 q1
Thus you can't take the decision of which path has to be followed for deriving the given string.
Definition of NFA:
The NFA can be formally defined as a collection of 5-tuples.
- Q is a finite set of states.
- Σ is a finite set of inputs.
- δ is called next state or transition function.
- q0 is initial state.
- F is a final state where F ⊆ Q .
Difference between DFA and NFA :
 |
| Difference between DFA and NFA |
Language of NFA :
We can construct a NFA for the given language. Following are the examples that show how to build NFA for any given language.
Example: Construct a NFA for the language, L1 = { consisting a substring 0 1 0 1 }, L2 ={ an bn }.
Solution: We will consider L1 first to design NFA. There can be any combination of 0 and 1 in the language but a substring 0101 must be present. We will get such a substring then it leads to a final state or accept state.
Thus is a NFA as for 0 input we have two different paths one going to q0 and other is going to q1.
The String 00010101 is acceptable by above given NFA and it is as shown below.
00010101 is accepted as q4 is final state.
Now we will build a NFA for L2. The language L2 is a language in which there be any number of a's or any number of b's. It accepts {a, b, aa, bb, aaa, bbb .....}.
Hence the NFA will be
The NFA shows two different state q1 and q2 for the input ε from q0 state. Here ε (pronounced as epsilon ) is basically a null move i.e. a move carrying no symbol from input set Σ. But a state change occurs from one state to other.
What is Finite Automata?|| DFA , NFA ||
Reviewed by For Learnig
on
April 24, 2023
Rating:
Reviewed by For Learnig
on
April 24, 2023
Rating:
No comments:
If you have any doubts, please tell me know